I just wanted to post the analogy I used in class to describe the difference between random and scale-free networks.  Imagine, if you will, that you need to roll a 12 in a game of Monopoly to get to the ‘Go’ square.  If you were using a twelve-sided die, you would have a 1/12 probability of success but because most games use two six-sided die then your probability drops to 1/36 simply because there are more possible outcomes:

For a twelve-sided die:

1|1

2|2

3|3

4|4

5|5

6|6

7|7

8|8

9|9

10|10

11|11

12|12

For two six-sided dice:

2|1-1

3|2-1, 1-2

4|1-3, 3-1, 2-2

5|1-4, 4-1, 2-3, 3-2

6|1-5, 5-1, 2-4, 4-2, 3-3

7|1-6, 6-1, 2-5, 5-2, 3-4, 4-3

8|2-6, 6-2, 3-5, 5-3, 4-4

9|3-6, 6-3, 4-5, 5-4

10|4-6, 6-4, 5-5

11|5-6, 6-5

12|6-6

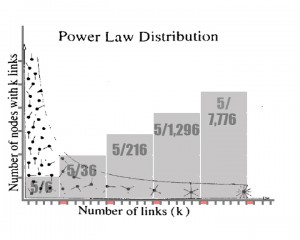
With the introduction of more elements the bell curve becomes more pronounced.  This also represents an interesting feature of random networks.  In a random network, a key requirement is that – because they are random – each node is equally probable to connect to any other node.  As such, outliers will exist (such as rolling a twelve), though this cannot account for the extraordinary popularity of certain sites.  Hubs like Facebook and Google should have an equiprobable chance of appearing as sites with only one or two links.  Take the rolls as the number of links to a specific site – if the Internet functioned as a random network you would expect it to represent a bell curve rather than the logarithmic curve described by Barabási.

A scale-free network relies on growth and preferential attachment.  We can also use basic probabilities to account for these networks, though we must change the way these probabilities function.

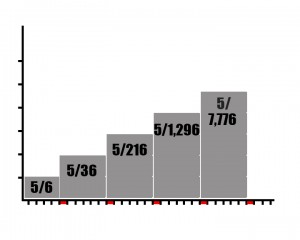
If you roll a double in Monopoly, you get to roll again.  Your odds of rolling a double are one in six.  It is possible to keep rolling doubles continuously but the probability reduces dramatically every time. (Well, not really.  It’s the same each individual time but in terms of the calculated probability of all rolls it reduces exponentially the more you get.)  The statistics overlaid on the graph below indicates how many of all possible outcomes exist within each section (ie, 5/6 turns will only receive one roll, 5/36 will have two, etc.)

To demonstrate how this can account for scale-free networks, let’s take a different game of Monopoly.  In this game, every time someone lands on your property, you get a chance to roll again, acquiring more property and hence more chances to keep rolling.  How many rolls (or links) are you likely to acquire over the course of the game?  What if the game had potentially infinite players and potentially infinite squares?

On the Internet, each link to a website increases the exposure of that website and consequently the probability that other users will see and link to it.  Of course it does not function as a static, one-in-six probability.  There are modifiers based on the perceived value of the content that affect the probabilities of growth.  However, you can see how, based on simple probabilities, hubs can emerge naturally simply due to exposure.  To illustrate this, I’ve overlaid the graph from above over the power law distribution graph from the Barabási reading:

(Link)