Whilst I realise the relevance of this text to the Internet’s networked system, I purposefully chose not to study physics and mathematics to avoid content like this! Somehow it has managed to work its way into my communications degree and I can safely say I am not a fan!

Putting my frustrations aside, I attempted to make sense of the information that this reading divulged. It firstly discusses Pareto’s 80/20 rule, a model sparked by the simple observation that ‘ 80% of his peas were produced by only 20% of the peapods.’ This rule has been found to apply to a wide range of other truisms, in and out of nature.

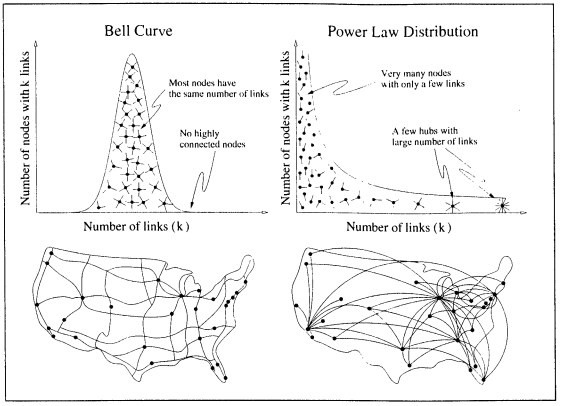
To my understanding, the 80/20 rule, when graphed mathematically, forms a ‘power law distribution.’ Unlike a random network, which is represented by a traditional bell curve, a power law distribution does not have a peak, and instead forms a continuously decreasing curve, implying that ‘many small events coexist with a few large events.’ This is supposedly the distinguishing feature of a power law. This diagram, sourced from the reading, really explained it for me:

So what does this have to do with the networked system of the Internet? Although I’m still attempting to get my head around this myself, here’s my understanding. It has recently been discovered that networks, like that of the Internet, do in fact follow a power law system, when previously thought to assume an entirely random structure.

The academics who discovered this used ‘a little robot’ (not sure if that means a literal little robot or something else too sciencey for my comprehension) to map out the nodes and links behind the Web and understand the complexity of it’s network once and for all. Whilst they assumed that the majority of documents would be equally popular, it was instead found that there were many nodes with a few links only, and a few ‘hubs’ with a extraordinary amount of links. This indicated for the first time that networks are far from random.

To me, this seems logical and I’m not sure why it was such a surprise to these academics. There are SO many websites out there that I would assume the majority of them would encounter minimal traffic, resulting from their mere number of links to other ‘nodes’ or webpages. But co-exisiting with these are a few immensely popular websites, like Facebook for example, that have millions of visitors each day due to their greater amount of links.

Am I missing something, or is it that simple?